Research

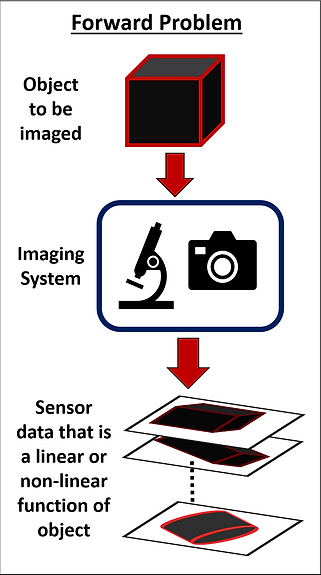
Formulating Forward Models

My research involves formulating mathematical models for imaging systems that allows us to simulate the sensor data given information of the object and imaging conditions. The dependence of sensor data on the object morphology can either be a straightforward linear relationship or a complex non-linear relationship. I have formulated such mathematical models, also called forward models, for a wide range of computational imaging modalities such as,

X-ray/electron computed tomography
X-ray phase contrast imaging
Magnetic vector-field electron tomography
X-ray dual-energy and multi-spectral imaging

The ultimate goal of such models is to solve the associated inverse problem of computationally reconstructing the underlying object from sensor data.

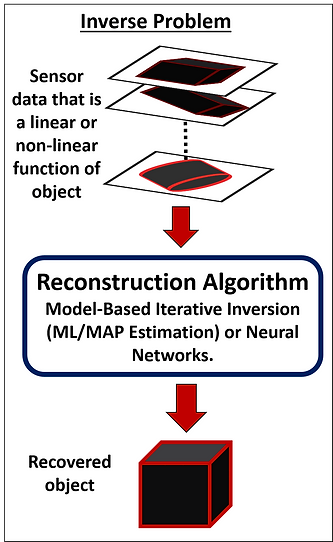
Solving Inverse Problems

The main goal of my research is to solve inverse problems associated with recovery of object image from sensor data. The dependence of sensor data on the object values might be linear or non-linear and might be known or unknown. The challenge is to recover the object even in the presence of noise and inadequate number of data samples.

My approach to solving inverse problems is to use -

Model-based inversion techniques based on maximum likelihood or maximum a posteriori estimation theory
Deep neural networks

Model-based approaches rely on gradient based optimization algorithms for reconstruction. This approach is used when the forward problem can be expressed in an analytical form. Neural networks are a great alternative when the forward model is unknown or the sensor data is severely under sampled.